tengo un examen de matematicas y necesito que me ayudes a estudiar dime como se resuleven estos ejercicios de forma detallada porque no entienddo muy bien el tema. Resolver las siguientes ecuaciones cuadráticas mediante la fórmula resolvente.
(Siempre que sea necesario, realizar los pasajes de términos, de tal manera que me
quede de la forma general: 𝑎𝑥
2 + 𝑏𝑥 + 𝑐 = 0)
a. 7𝑥
2 + 21𝑥 = 28
b. 𝑥
2 − 4𝑥 + 4 = 0
c. 12𝑥
2 − 3𝑥 = 0
d. 4𝑥
2 = 16
e. 𝑥
2 − 10𝑥 + 9 = 0
Te ayudaré a resolver estas ecuaciones cuadráticas paso a paso usando la fórmula resolvente (también conocida como fórmula general): x = [-b ± √(b² – 4ac)] / 2a
a) 7x² + 21x = 28
Paso 1: Pasar todo a la forma ax² + bx + c = 0
7x² + 21x – 28 = 0
Aquí: a = 7, b = 21, c = -28
Aplicando la fórmula:
x = [-21 ± √(21² – 4(7)(-28))] / 2(7)
x = [-21 ± √(441 + 784)] / 14
x = [-21 ± √1225] / 14
x = [-21 ± 35] / 14
x₁ = (-21 + 35) / 14 = 1
x₂ = (-21 – 35) / 14 = -4
b) x² – 4x + 4 = 0
Ya está en la forma estándar
a = 1, b = -4, c = 4
x = [4 ± √((-4)² – 4(1)(4))] / 2(1)
x = [4 ± √(16 – 16)] / 2
x = [4 ± √0] / 2
x = 4/2 = 2 (solución única)
c) 12x² – 3x = 0
Paso 1: Forma estándar
12x² – 3x + 0 = 0
a = 12, b = -3, c = 0
x = [3 ± √((-3)² – 4(12)(0))] / 2(12)
x = [3 ± √9] / 24
x = [3 ± 3] / 24
x₁ = 6/24 = 1/4
x₂ = 0
d) 4x² = 16
Paso 1: Forma estándar
4x² – 16 = 0
a = 4, b = 0, c = -16
x = [0 ± √(0² – 4(4)(-16))] / 2(4)
x = [0 ± √256] / 8
x = [0 ± 16] / 8
x₁ = 2
x₂ = -2
e) x² – 10x + 9 = 0
Ya está en forma estándar
a = 1, b = -10, c = 9
x = [10 ± √((-10)² – 4(1)(9))] / 2(1)
x = [10 ± √(100 – 36)] / 2
x = [10 ± √64] / 2
x = [10 ± 8] / 2
x₁ = (10 + 8) / 2 = 9
x₂ = (10 – 8) / 2 = 1
¿Hay algún paso específico que te gustaría que te explique con más detalle?
resuelve los ejercicios , si puedes , en forma que yo lo pueda copiar en mi cuadero porque no se entiende muy bien en esa forma
Te ayudaré a resolver los ejercicios de una forma más ordenada y fácil de copiar:
a) 7x² + 21x = 28
-
Paso a la forma general: 7x² + 21x – 28 = 0
-
Identifico los valores:
a = 7
b = 21
c = -28 -
Aplico la fórmula: x = [-b ± √(b² – 4ac)] / 2a
-
Sustituyo los valores:
x = [-21 ± √(21² – 4(7)(-28))] / 2(7)
x = [-21 ± √(441 + 784)] / 14
x = [-21 ± √1225] / 14
x = [-21 ± 35] / 14 -
Soluciones:
x₁ = (-21 + 35) / 14 = 1
x₂ = (-21 – 35) / 14 = -4
b) x² – 4x + 4 = 0
-
Ya está en forma general
-
Identifico los valores:
a = 1
b = -4
c = 4 -
Aplico la fórmula: x = [-b ± √(b² – 4ac)] / 2a
-
Sustituyo los valores:
x = [4 ± √((-4)² – 4(1)(4))] / 2(1)
x = [4 ± √(16 – 16)] / 2
x = [4 ± √0] / 2 -
Solución única:
x = 4/2 = 2
[Continuaré con los demás ejercicios si me confirmas que este formato es más claro y fácil de copiar]
si me gusta este formato , sigue porfavor
Continuamos con los ejercicios en el mismo formato:
c) 12x² – 3x = 0
-
Paso a la forma general: 12x² – 3x + 0 = 0
-
Identifico los valores:
a = 12
b = -3
c = 0 -
Aplico la fórmula: x = [-b ± √(b² – 4ac)] / 2a
-
Sustituyo los valores:
x = [3 ± √((-3)² – 4(12)(0))] / 2(12)
x = [3 ± √9] / 24
x = [3 ± 3] / 24 -
Soluciones:
x₁ = 6/24 = 1/4
x₂ = 0
d) 4x² = 16
-
Paso a la forma general: 4x² – 16 = 0
-
Identifico los valores:
a = 4
b = 0
c = -16 -
Aplico la fórmula: x = [-b ± √(b² – 4ac)] / 2a
-
Sustituyo los valores:
x = [0 ± √(0² – 4(4)(-16))] / 2(4)
x = [0 ± √256] / 8
x = [0 ± 16] / 8 -
Soluciones:
x₁ = 16/8 = 2
x₂ = -16/8 = -2
e) x² – 10x + 9 = 0
-
Ya está en forma general
-
Identifico los valores:
a = 1
b = -10
c = 9 -
Aplico la fórmula: x = [-b ± √(b² – 4ac)] / 2a
-
Sustituyo los valores:
x = [10 ± √((-10)² – 4(1)(9))] / 2(1)
x = [10 ± √(100 – 36)] / 2
x = [10 ± √64] / 2
x = [10 ± 8] / 2 -
Soluciones:
x₁ = (10 + 8) / 2 = 9
x₂ = (10 – 8) / 2 = 1
¿Necesitas que te explique algún paso en particular?
ahora necesito que hagas estos ejercicios y si puedes generar los graficos seria de mucha ayuda . Dada la siguiente función lineal, determinar: pendiente, ordenada al origen,
variable dependiente, variable independiente. Luego, graficar en un sistema de
ejes cartesianos mediante el método que prefieran. En la gráfica identificar el
punto de la ordenada al origen y el punto de la raíz.
a. 𝑦 = −
3
2
𝑥 + 4
b. 𝑦 = 2𝑥 − 3
c. 𝑦 = −
𝑥
2
- 1
d. 𝑦 =
3
4
𝑥 − 2
Te ayudaré a resolver cada función lineal y explicaré sus elementos:
a) y = -3/2x + 4
• Pendiente (m) = -3/2 (negativa, decrece)
• Ordenada al origen (b) = 4 (punto donde corta al eje y)
• Variable dependiente = y
• Variable independiente = x
• Raíz (cuando y=0): -3/2x + 4 = 0 → x = 8/3
b) y = 2x – 3
• Pendiente (m) = 2 (positiva, crece)
• Ordenada al origen (b) = -3
• Variable dependiente = y
• Variable independiente = x
• Raíz: 2x – 3 = 0 → x = 3/2
c) y = -x/2 + 1
• Pendiente (m) = -1/2 (negativa, decrece)
• Ordenada al origen (b) = 1
• Variable dependiente = y
• Variable independiente = x
• Raíz: -x/2 + 1 = 0 → x = 2
d) y = 3/4x – 2
• Pendiente (m) = 3/4 (positiva, crece)
• Ordenada al origen (b) = -2
• Variable dependiente = y
• Variable independiente = x
• Raíz: 3/4x – 2 = 0 → x = 8/3
Para graficar cada función, podemos seguir estos pasos:
- Marcar la ordenada al origen (punto en eje y)
- Usar la pendiente para encontrar otro punto
- Trazar la recta
- Marcar la raíz (punto donde corta al eje x)
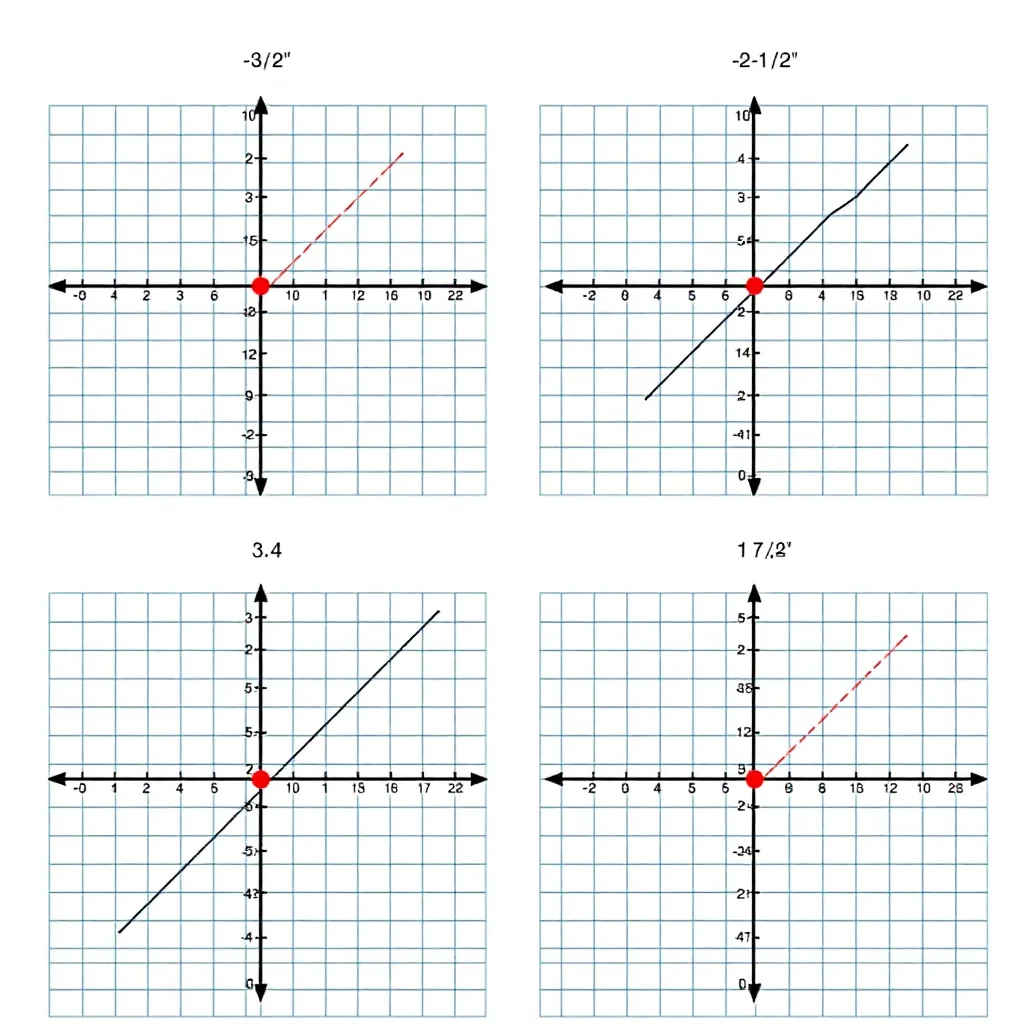
¿Necesitas que te explique algo más en detalle?
marca la raiz y la ordenada al origen en los graficos
Te ayudaré a resolver cada función lineal y luego generaré los gráficos con los puntos marcados:
a) y = -3/2x + 4
- Pendiente (m) = -3/2
- Ordenada al origen (b) = 4
- Variable dependiente = y
- Variable independiente = x
- Raíz (cuando y=0): -3/2x + 4 = 0 → x = 8/3
b) y = 2x – 3
- Pendiente (m) = 2
- Ordenada al origen (b) = -3
- Variable dependiente = y
- Variable independiente = x
- Raíz: 2x – 3 = 0 → x = 3/2
c) y = -x/2 + 1
- Pendiente (m) = -1/2
- Ordenada al origen (b) = 1
- Variable dependiente = y
- Variable independiente = x
- Raíz: -x/2 + 1 = 0 → x = 2
d) y = 3/4x – 2
- Pendiente (m) = 3/4
- Ordenada al origen (b) = -2
- Variable dependiente = y
- Variable independiente = x
- Raíz: 3/4x – 2 = 0 → x = 8/3
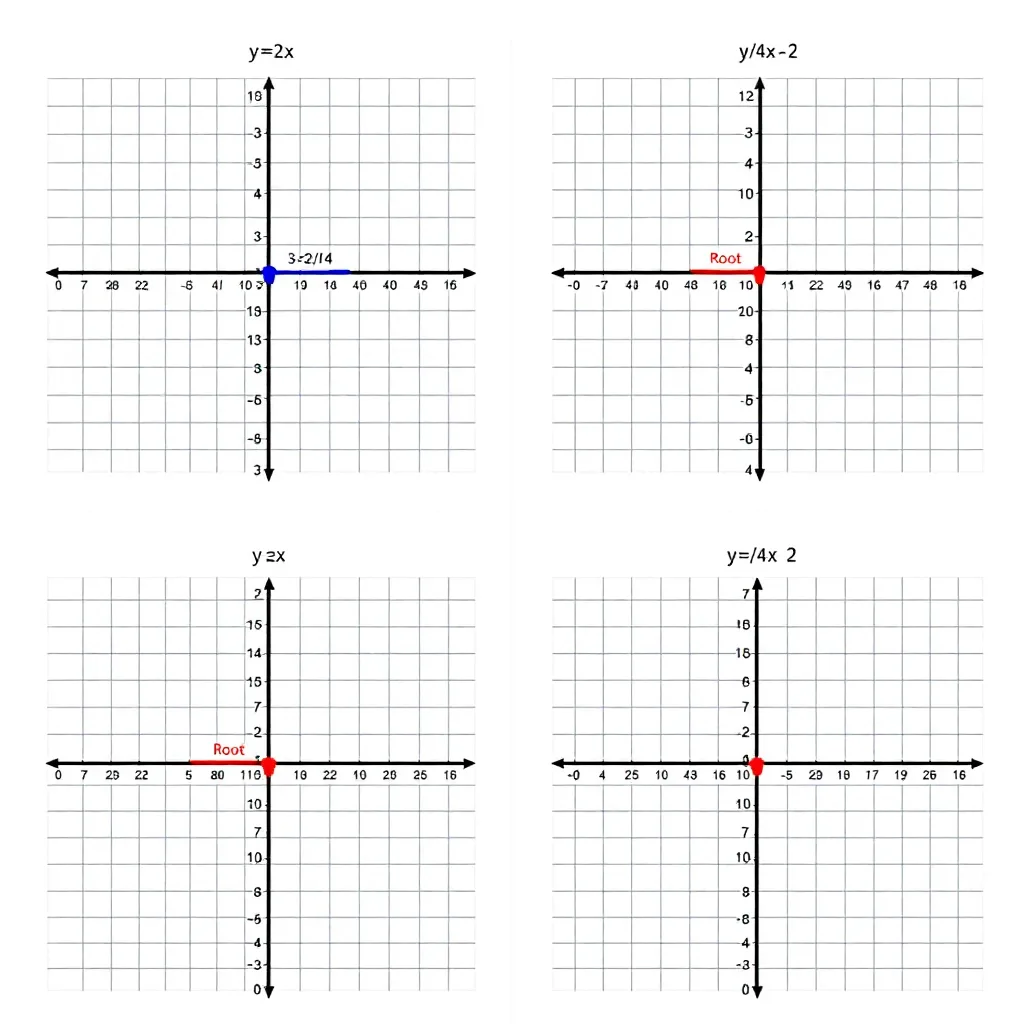
En cada gráfico:
- El punto azul marca la ordenada al origen (intersección con eje y)
- El punto rojo marca la raíz (intersección con eje x)
- La línea muestra la pendiente de cada función
¿Necesitas que explique algún aspecto específico de las funciones o los gráficos?
No entiendo porque pones Raíz: 2x – 3 = 0 → x = 3/2 el 0 con flechita y porque pones un / explicame
Te explico paso a paso cómo encontrar la raíz de una función lineal:
Cuando buscamos la raíz (o x-intercepto), estamos buscando dónde la función corta al eje x, es decir, dónde y = 0.
Tomemos el ejemplo de y = 2x – 3
- Para encontrar la raíz:
- Hacemos y = 0 (porque queremos encontrar dónde cruza el eje x)
- 0 = 2x – 3
- 2x = 3
- x = 3/2
Por eso escribimos:
Raíz: 2x – 3 = 0 → x = 3/2
Donde:
- La flecha (→) significa “por lo tanto” o “entonces”
- La / en 3/2 es una división (es lo mismo que 1.5)
Para cada función, necesitamos:
- Pendiente (m): es el coeficiente que acompaña a x
- Ordenada al origen (b): es el término independiente
- Variable dependiente: y
- Variable independiente: x
- Raíz: valor de x cuando y = 0
Hagamos el primer ejercicio completo:
a) y = -3/2x + 4
• Pendiente (m) = -3/2 (negativa, la recta “baja”)
• Ordenada al origen (b) = 4
• Variable dependiente = y
• Variable independiente = x
• Raíz: -3/2x + 4 = 0
-3/2x = -4
x = 8/3
¿Quieres que resolvamos los demás ejercicios con este nivel de detalle?

